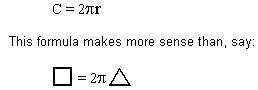Math problem solver

Get free pre algebra problems

Algebra is a branch of mathematics concerning the study of structure, relation, and quantity. Together with geometry, analysis, combinatory, and number theory, algebra is one of the main branches of mathematics. Elementary algebra is often part of the curriculum in secondary educations. In this article, we are going lean to about step by step explanation for I need help with pre algebra. Also get help with pre algebra answers solved

Solve the given equations and find out the x value 6x – 7 = 11

Solution:

Find out the x value of the given linear equation.

We are move the -7 into the right side, we get

6x = 11 + 7

6x = 18.

X = 3

The x value of the given equation is 3.

Our next post will be on free pre algebra homework help

Understanding volume of sphere formula

Introduction to volume of sphere formula using diameter:
Volume of a sphere formula using diameter article deals with the volume formula of the sphere using diameter and the model problems related to volume of the sphere.
Definition of volume of a sphere
The volume or capacity occupied by the sphere. The volume of the sphere is measured in cube units.The sphere is three-dimensional shape.here diameter is twice the length of the radius of the sphere, you can get help with trigonometric integrals
Generally the volume of a solid is calculated as the area of the base times its height as long the area is constant throughout the height of the solid. But this concept can not be directly applied to find the volume of a sphere because the area changes with every cross section of the sphere.
Archimedes, the famous mathematician, engineer and scientist around the year 250 B.C framed a formula, which after many centuries was proved to be right.
Hope you liked our post, get help with Ordered Pair

Understanding math formula one

Let us learn how math formula one works

The mathematical formulas are very useful to calculate the values. These are formulas for algebra, Formulas for percentage, profit and loss, Ratio and Proportions and formulas for area and perimeter.

MATHEMATICAL FORMULAS IN ALGEBRA:
1. N natural numbers formula = n (n+1)/2
2. Squares of first n natural numbers = n (n+1) (2n+1)/6
3. Cubes of first n natural numbers = [n (n+1)/2]²
4. Natural n number (odd) = n²
5. Average = (Sum of the items)/ Total Number of items.
Arithmetic Progression (A.P.): An A.P. is of the form a, a+d, a+2d, a+3d, Where a is called the 'first term' and d is called the 'common difference'
1. N^th term of an A.P is giev as , t_n = a + (n-1) d
2. Sum of the first n terms of an A.P si gievn as, S_n = n/2[2a+ (n-1) d] or S_n = n/2(first term + Last term)
Geometrical Progression (G.P.): A G.P. is of the form a, a r, a r², a r³,... Where a is called the 'first term' and r is called the 'common ratio'.
1. N^th term of a G.P is given as, tn = a r^n-1
2. Sum of the first n terms in a G.P is given as, Sn = a|1-r n|/|1-r|

What is Decimal to Fraction Calculator

This decimal to fraction calculator will quickly convert any decimals to a fraction in a split of a second
Some decimals are called repeating decimals or recurring decimals. Other decimals are called terminating decimals.

Steps for decimal to fraction calculator:

• Step 1: first divided by 1, for the given decimal value.
• Step 2: multiply both sides by 10 for whole number after the decimal point. ( Example, there is two number after the decimals means, using 100, there is three number after the decimals value means, using 1000, etc).
• Step 3: get the last solution, which reduce the fraction.

Inequalities

Inequalities Rules

a <> means a is less than b (so b is greater than a)

a ≤ b means a is less than or equal to b (so b is greater than or equal to a)

a ≥ b means a is greater than or equal to b etc.

a > b means a is greater than b etc.

If you have an inequality, you can add or subtract numbers from each side of the inequality, as with an equation. You can also multiply or divide by a constant. However, if you multiply or divide by a negative number, the inequality sign is reversed.

Example

Solve 3(x + 4) <>

3x + 12 <>

∴ -2x < -3

∴ x > 3/2 (note: sign reversed because we divided by -2)

Inequalities can be used to describe what range of values a variable can be.

E.g. 4 ≤ x <>

Graphs

Inequalities are represented on graphs using shading. For example, if y > 4x, the graph of y = 4x would be drawn. Then either all of the points greater than 4x would be shaded or all of the points less than or equal to 4x would be shaded.

Example

x + y <>

and 1 <>

Represent these inequalities on a graph by leaving un-shaded the required regions (i.e. do not shade the points which satisfy the inequalities, but shade everywhere else).

Number Lines

Inequalities can also be represented on number lines. Draw a number line and above the line draw a line for each inequality, over the numbers for which it is true. At the end of these lines, draw a circle. The circle should be filled in if the inequality can equal that number and left unfilled if it cannot.

Example

On the number line below show the solution to these inequalities.

-7 ≤ 2x - 3 <>

This can be split into the two inequalities:

-7 ≤ 2x - 3 and 2x - 3 <>

∴ -4 ≤ 2x and 2x <>

∴ -2 ≤ x and x <>

The circle is filled in at -2 because the first inequality specifies that x can equal -2, whereas x is less than (and not equal to) 3 and so the circle is not filled in at 3.

The solution to the inequalities occurs where the two lines overlap, i.e. for -2 ≤ x <>

Variables

Definition Of Variable
What is a variable? It is a box, and it exists to contain a value. Sometimes the value is already inside the box, and you have to figure out what that value is. Other times, the box is empty, and you get to pick the value to put inside. More about that later. First...
Remember when you were in elementary school, and you were learning your addition? The teacher would hand you worksheets that said things like:

fill in the box.

Variables are the same thing. Now we say:

x + 2 = 5 ; solve for x.

Why did we switch from boxes to letters? Because letters are better. Boxes come in only a few shapes, but letters come in many varieties, and letters can stand for something. For instance, the formula from geometry for finding a circle's circumference is:

The two formulae say exactly the same thing, but using "C" for "circumference" and "r" for "radius" is more useful than using "square" and "triangle", respectively. Boxes are fine, but letters are better.

---

In the above discussion, I illustrated both uses of variables. In the equation "x + 2 = 5", x can only have a value of 3. The statement (the equation) is not true for any other value. That is to say, the value of x is "fixed"; we just have to figure out what it is.
On the other hand, in the equation "C=2πr" the radius r can be any non-negative number we choose — we get to pick! — and then we get to figure out what the circumference C is. In the first case, we had to open the box to see what was already inside; in the second, we got to put the value in ourselves.
Now that we have variables, what do we do with them? Go back in your mind again to elementary school: Your teacher would have you add "2 apples plus 6 apples is 8 apples". The same rules apply to variables: "2 boxes plus 6 boxes is 8 boxes", or, using variables, "2x + 6x = 8x". "A box and another box is two boxes", or "x + x = 2x". "Two dollars, less the ten that you owe to your friend, means that you're eight dollars in the red", or "2x – 10x = –8x".
But note: "2 apples plus 6 oranges" is just 2 apples and 6 oranges; they might make a nice fruit salad, but they're not 8 of anything. In the same way, "2x + 6y" is just 2x + 6y; you can't combine the two variables into one. Copyright ©
When multiplying, we use exponents. For instance, (5)(5) = 5². Of course, we can simplify this as 5² = 25. Similarly, (x)(x) = x². But, until we know what value to put in for x, we cannot simplify this.
Don't confuse multiplication and addition: (x)(x) does not equal 2x, just as (5)(5) does not equal (2)(5); instead, (x)(x) equals x². (Note the technique I just used: If you're not sure what to do with the variables, put in numbers, where you know what to do. Then, whatever you did with the numbers, do that with the variables.)